This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Vitor da Fonseca, Instituto de Astrof´ısica e Ciˆencias do Espa¸co, Faculdade de Ciˆencias da Universidade de Lisboa;
(2) Tiago Barreiro, Instituto de Astrof´ısica e Ciˆencias do Espa¸co, Faculdade de Ciˆencias da Universidade de Lisboa and 2ECEO, Universidade Lus´ofona;
(3)Nelson J. Nunes, Instituto de Astrof´ısica e Ciˆencias do Espa¸co, Faculdade de Ciˆencias da Universidade de Lisboa.
Table of Links
- Abstract and Intro
- Coupling Dark Energy to Neutrinos
- Impact of the Coupling on Perturbations and Observables
- Parameter Estimation
- Discussion
- Acknowledgment, Appendix, and References
II. COUPLING DARK ENERGY TO NEUTRINOS
Let us consider a flat universe with vanishing curvature, spatially homogeneous and isotropic, whose expansion is parameterized by the scale factor a associated with the Friedmann-Lemaˆıtre-Roberson-Walker (FLRW) spacetime metric. Further considering that the expansion is sourced by photons (γ), baryons (b), cold dark matter (c), neutrinos (ν) and a scalar field dark energy (ϕ) responsible for the current acceleration, the Friedmann equation reads

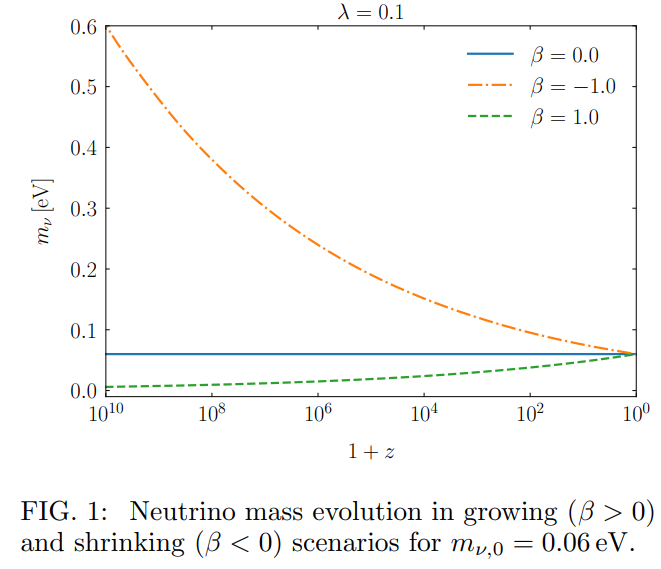
In this study, we want to test a possible interaction between neutrino species and dark energy, in a mass-varying neutrino model where active neutrinos are coupled to the scalar field [13–20]. Because to leading order cosmological data are only sensitive to the total neutrino mass [36, 37], we assume for practical purposes [38] two massless neutrinos and a massive neutrino non-minimally coupled to the quintessence component. The coupled neutrino has a varying effective mass, which depends on the value of the scalar field and on a dimensionless and constant parameter β,

The stress energy tensors of the neutrino fluid and the scalar field are not conserved separately. We have

where pϕ is the pressure in the field. The extra source terms vanish without interaction, β = 0, or if the massive neutrino particles are ultrarelativistic, behaving as traceless radiation.

To test the model with observations, we adopt a known phenomenological parametrization, first proposed in Ref. [22], where the scalar field depends linearly on the number of e-folds, N ≡ ln a, throughout the cosmological evolution. We introduce a dimensionless constant λ for the slope of the scaling:

This simple approach is a powerful alternative to the popular CPL parametrization [40, 41], since a large variety of dark energy equation of state evolutions can be captured by just one additional parameter [42], thereby limiting the degeneracies in Bayesian inferences. An additional advantage is that the scalar field potential can be reconstructed analytically following Ref. [22, 24–26]. This is done by solving the first-order differential equation (2.7) to find ρϕ using the constraint equation (2.1) and noting that ϕ˙ = λH according to Eq. (2.9). The potential happens to be a sum of exponential terms,
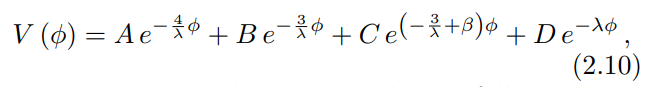
where the mass scales are given by the following analytical expressions,


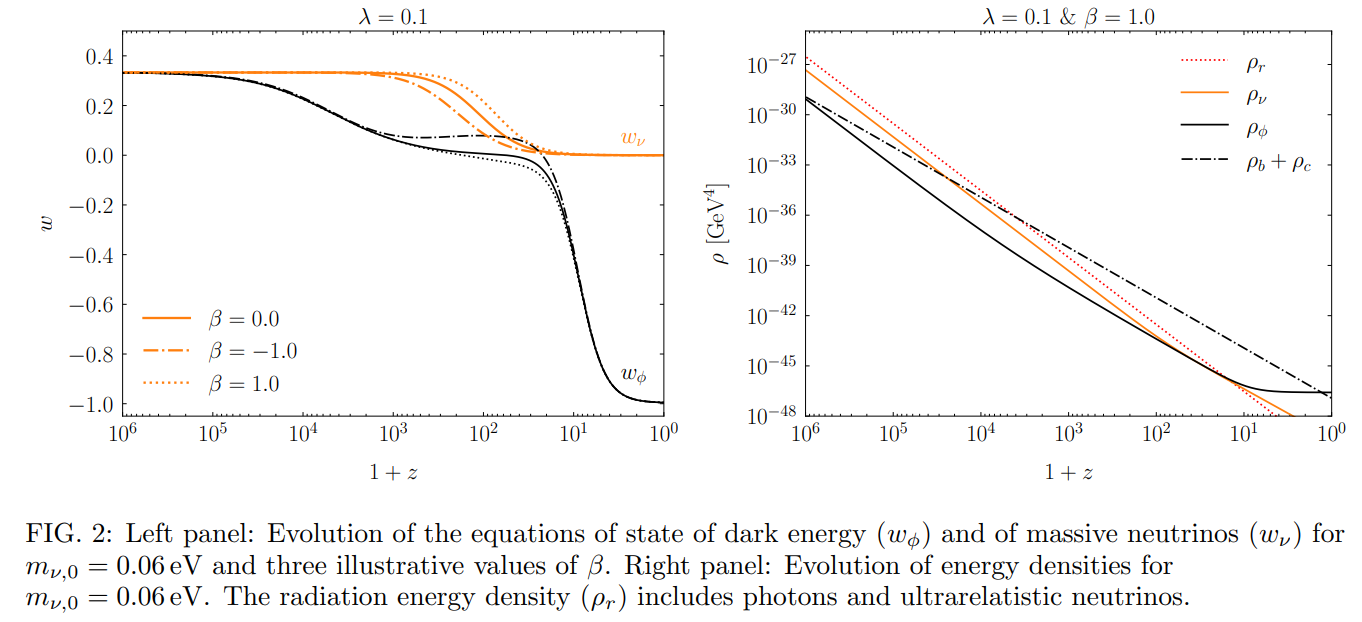
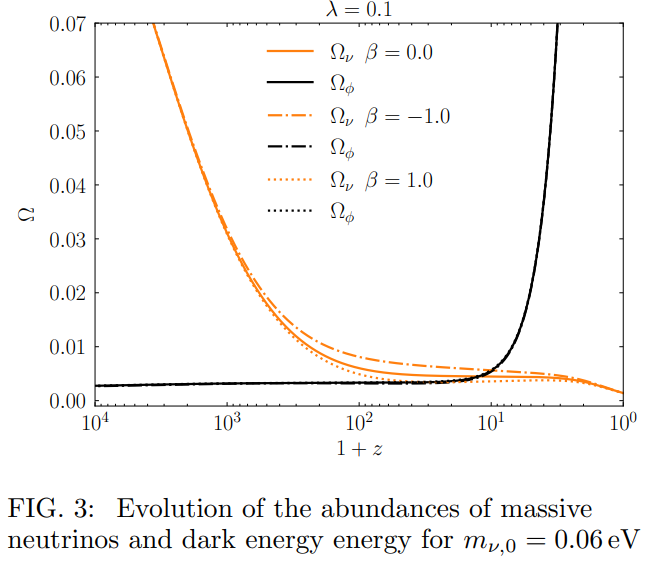
We can see from Fig. 2 that the coupling with neutrinos changes wϕ during the matter-dominated era. For growing masses (β > 0, dotted line), the field equation of state is smaller compared to the uncoupled case (β = 0, solid line). On the contrary, wϕ is larger when the energy transfer occurs in the opposite direction, i.e. from neutrinos of shrinking mass (β < 0, dash-dotted line). Correspondingly, Fig. 3 shows that the non-relativistic neutrinos which receive energy from the scalar field (β > 0) have lower fractional energy density to reach the same present mass than when they give energy (β < 0).

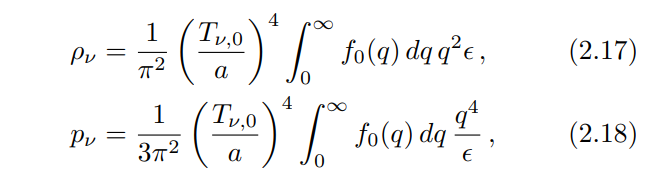
with
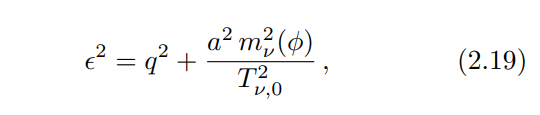
where ϵ is the neutrino comoving energy.