This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Z. Jennings, Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK (E-mail: z.jennings@keele.ac.uk);
(2) J. Southworth, Astrophysics Group, Keele University, Staffordshire, ST5 5BG, UK;
(3) K. Pavlovski, Department of Physics, Faculty of Science, University of Zagreb, 10000 Zagreb, Croatia;
(4) T. Van Reeth, Institute of Astronomy, KU Leuven, Celestijnenlaan 200D, B-3001 Leuven, Belgium.
Table of Links
- Abstract and Intro
- Observation
- Orbital Ephemeris
- Radial Velocity Analysis
- Spectral Analysis
- Analysis of the Light Curve
- Physical Properties
- Asteroseismic Analysis
- Discussion
- Conclusion, Data Availability, Acknowledgments, and References
- Appendix A: Ephemeris Determination
- Appendix B: Iteratively Prewhitened Frequencies
- Appendix C: Detected Tidally Perturbed Pulsations
8 ASTEROSEISMIC ANALYSIS
8.1 Frequency analysis
Following the binary modelling, we continue with the asteroseismic analysis of the target. Because the observed pulsations have much smaller amplitudes than the binary signal, the quality of the TESS and WASP data are insufficient for the asteroseismic analysis, and we limit ourselves to using the residual Kepler light curve. This is the merged light curve of all available Kepler short-cadence data after subtracting the best-fitting binary model, hereafter referred to as the pulsation light curve. To minimize the impact of outliers and instrumental effects on the asteroseismic analysis of small-amplitude pulsations, we apply additional processing to the data. Firstly, we remove those parts where coronal mass ejections (CMEs) or thermal and pointing changes of the spacecraft, such as at the start of a quarter or after a safe-mode event, have a visible impact on the quality of the light curve. Secondly, we apply preliminary iterative pre-whitening (as described by, e.g., Van Reeth et al. 2023) to build a tentative mathematical model of the 20 most dominant pulsations using a sum of sine waves


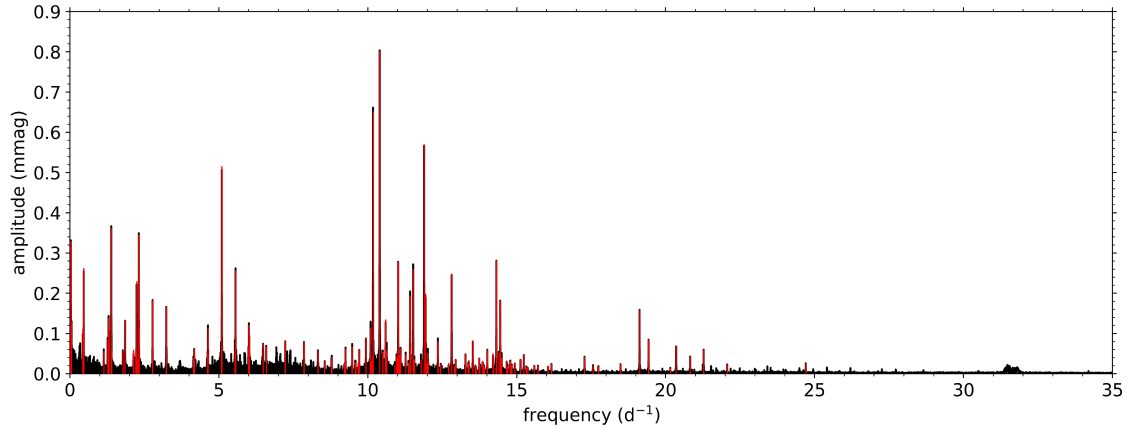
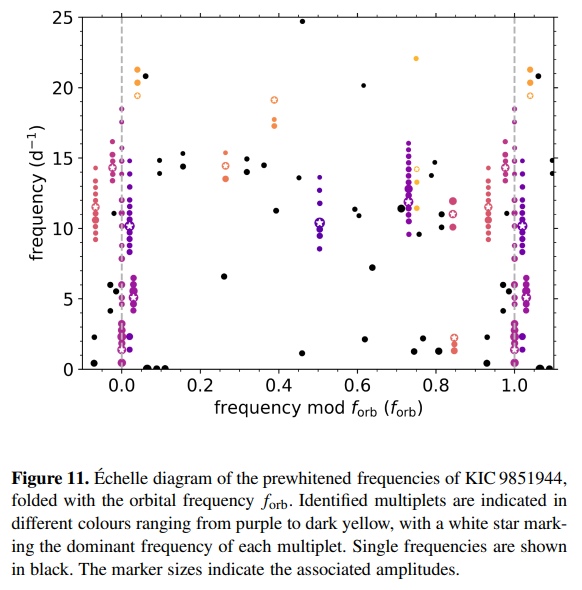
8.2 Tidal perturbation analysis



8.3 Orbital harmonic frequencies

As pointed out by Guo et al. (2016), the detection of an orbital harmonic frequency comb is somewhat unexpected for synchronised binaries with circular orbits, though it has also been detected for other such systems (da Silva et al. 2014). Because the orbital eccentricity of the binary is zero, the equilibrium tides that are responsible for deforming the star and perturbing the pulsations are considerably larger than the dynamical tides that excite oscillations. Hence, this can indicate that this system has a slightly eccentric orbit or that one or both of the components is asynchronously rotating, within the uncertainty margins of our measurements.
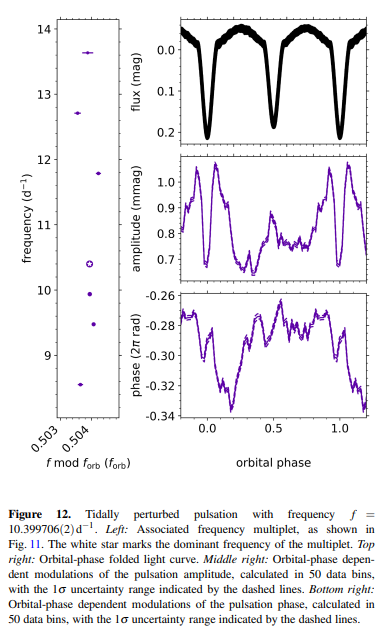
8.4 Gravity-mode period-spacing pattern

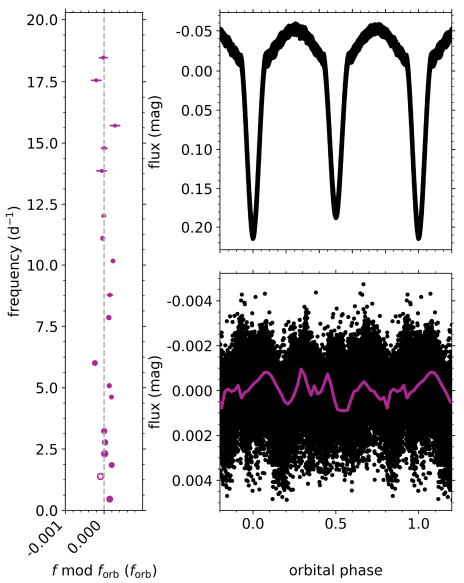

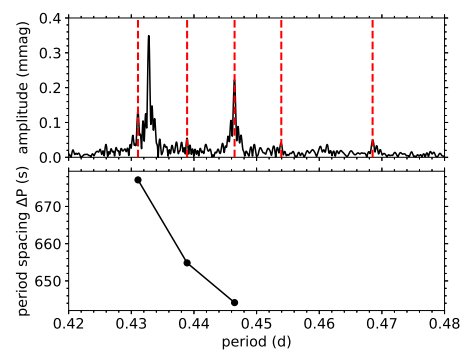
The error margins are smaller than the symbol sizes.
