Author:
(1) Attila Losonczi.
Table of Links
1.1 Basic notions and notations
1.2 Basic definitions from [7] and [8]
2 Generalized integral
2.1 Multiplication on [0, +∞) × [−∞, +∞]
2.3 The integral of functions taking values in [0, +∞) × [0, +∞)
2.3 The integral of functions taking values in [0, +∞) × [0, +∞)
We are now ready to define the integral in the promised more general context.
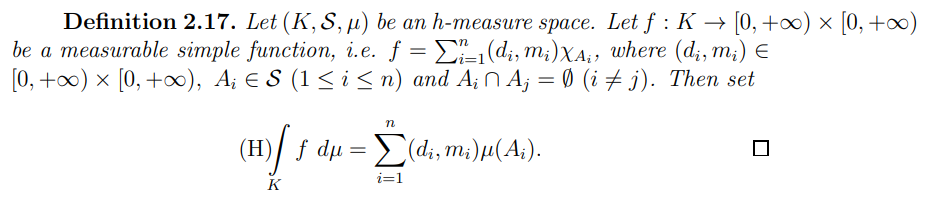
When building the theory of the integral, we then can follow the same way we had in subsection [8]?? and we can show that the integral of simple functions is well-defined, and having the required properties (see [8]??), and the integral provides an h-measure (see [8]??). For those, one has to observe only that in this more general context too, we only need that the multiplication is commutative, associative and distributive, and the properties in 2.3 and 2.9 hold. We just repeat those three statements without proofs; the reader can check them easily.
Proposition 2.18. The integral in definition 2.17 is well defined.
Proposition 2.19. Let (K, S, µ) be an h-measure space. Let f, g : K → [0, +∞)×[0, +∞) be measurable simple functions. Then the followings hold.
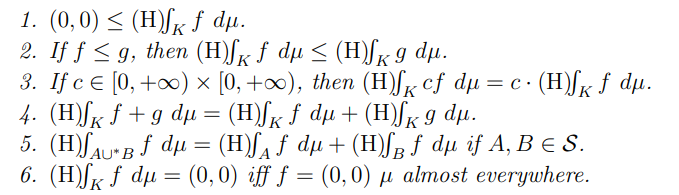
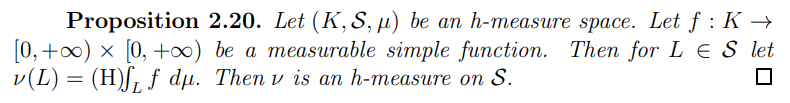
As in subsection [8]??, the next step is to define the integral of nonnegative functions.
Definition 2.21. Let (K, S, µ) be an h-measure space. Let f : K → [0, +∞) × [0, +∞) be a measurable function. Then set
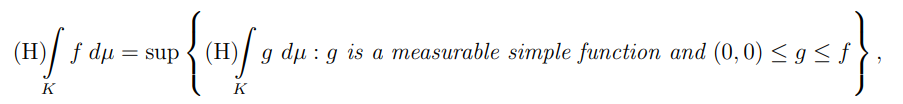
where a simple function takes its values from [0, +∞) × [0, +∞).


Now we are going to prove that the integral is additive.

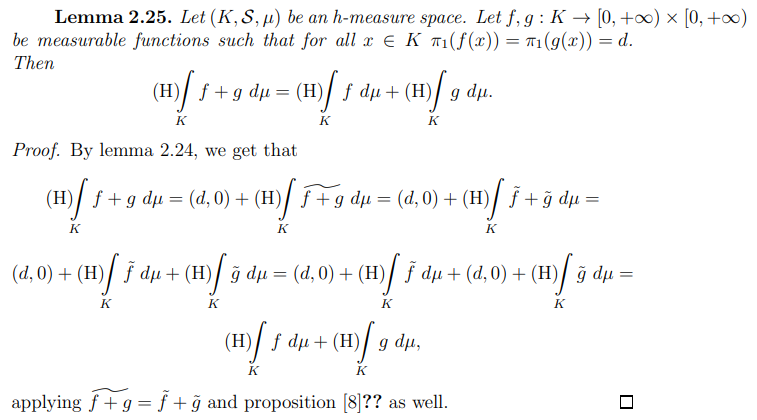
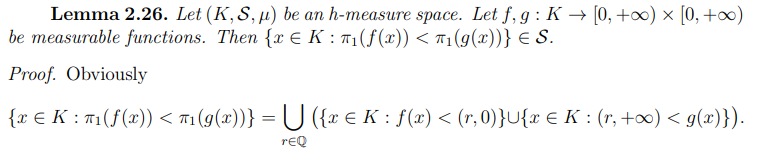
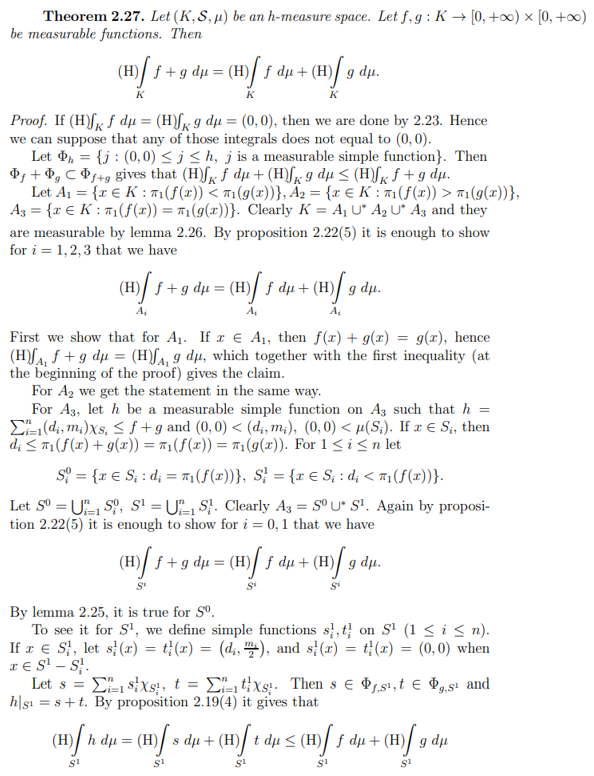
which yields that
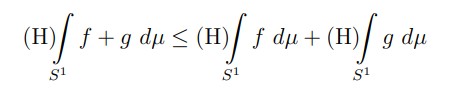
which together with the first inequality (at the beginning of the proof) gives the claim
Theorem 2.28. Let (K, S, µ) be an h-measure space. Let f : K → [0, +∞) × [0, +∞) be a measurable function. Then
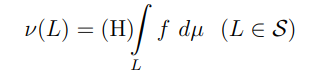
is an h-measure on S.
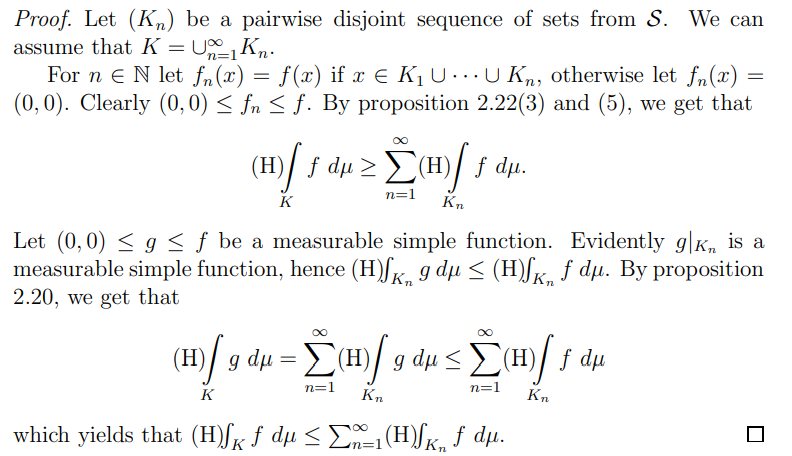

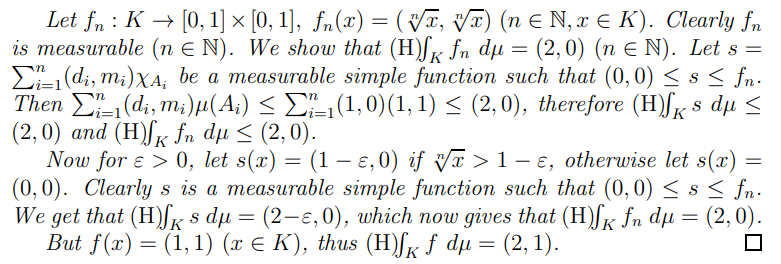
Remark 2.31. By remark 2.2, this integral is a natural generalization of the one described in [8]
Furthermore it also handles the case when f taking values from [0, +∞) × [0, +∞) and µ is an ordinary measure only: just apply proposition [8]??. The most natural embedding is when we have µ(S) = (0, ν(S)) (S ∈ S) for given measure ν on S.
Now we present a way how the integral can be calculated. First we need an extension of the notion of simple function where we allow that its second coordinate function takes +∞ as a value as well.
Definition 2.32. We call g : K → [0, +∞) × [0, +∞] an i-simple function if Rang is finite.
Lemma 2.33. Let (K, S, µ) be an h-measure space. Let f : K → [0, +∞) × [0, +∞) be a measurable function. Then

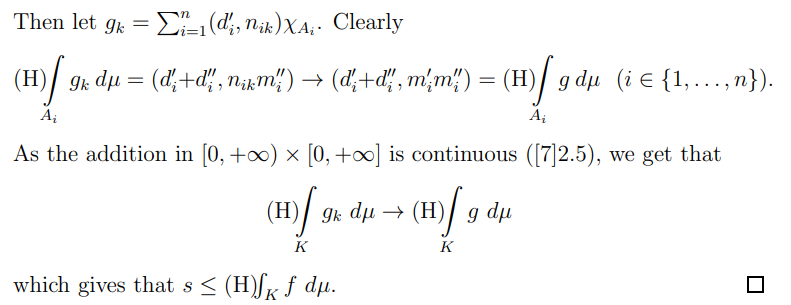
Theorem 2.34. Let (K, S, µ) be an h-measure space. Let f : K → [0, +∞) × [0, +∞) be a measurable function. Then

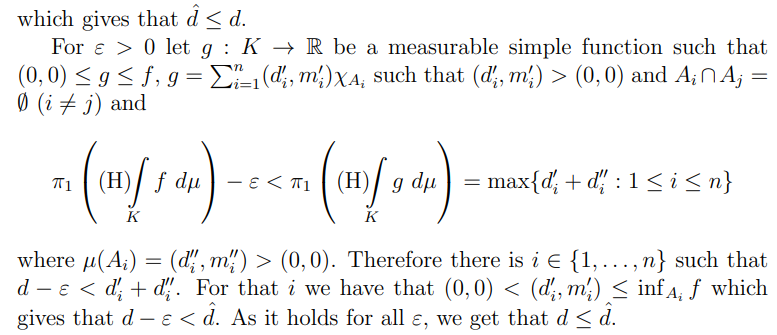
When validating the equality for the second coordinate, there are two cases.

Remark 2.35. Note that in the formulation of the theorem, inside the definition of d, the condition µ(L) > (0, 0) is essential, but inside the definition of m, the condition µ(Li) > (0, 0) can be omitted.
We can apply the previous theorem when µ is an ordinary measure.
Lemma 2.36. Let (K, S, ν) be a measure space. Let f : K → [0, +∞) be a measurable function. Then
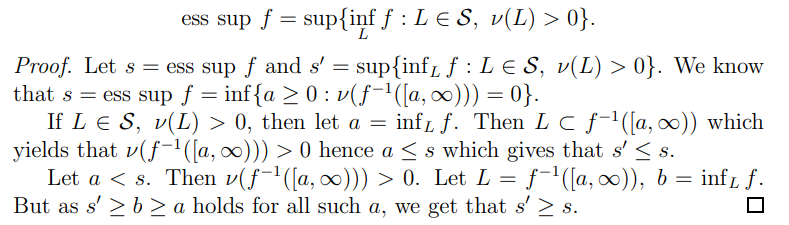
Theorem 2.37. Let (K, S, ν) be a measure space. Let f : K → [0, +∞) × [0, +∞) be a measurable function. Then
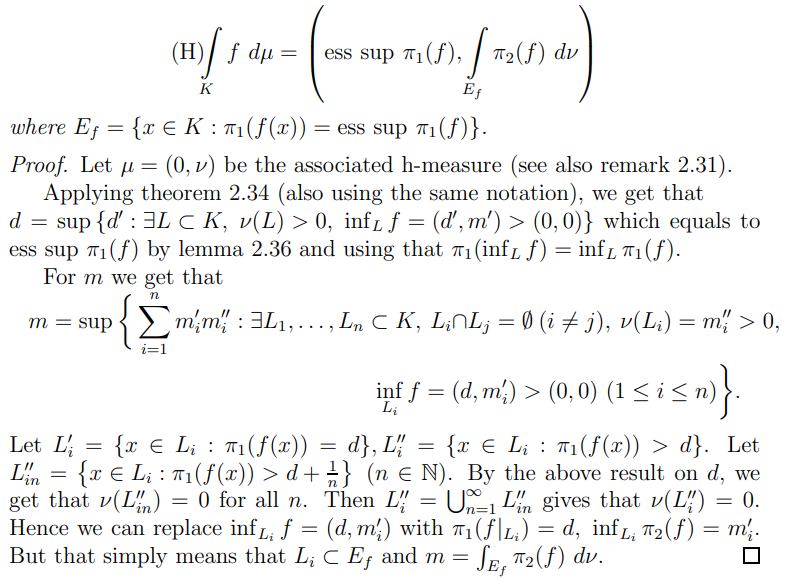
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.