Author:
(1) Attila Losonczi.
Table of Links
1.1 Basic notions and notations
1.2 Basic definitions from [7] and [8]
2 Generalized integral
2.1 Multiplication on [0, +∞) × [−∞, +∞]
2.3 The integral of functions taking values in [0, +∞) × [0, +∞)
1.1 Basic notions and notations
Here we enumerate the basics that we will apply throughout the paper.
For K ⊂ R, χK will denote the characteristic function of K i.e. χK(x) = 1 if x ∈ K, otherwise χK(x) = 0.
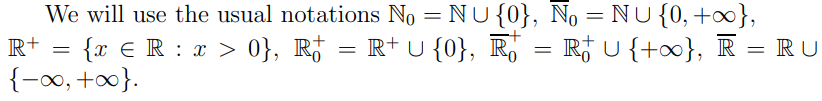
Some usual operations and relation with ±∞: (+∞)+(+∞) = +∞, (−∞)+ (−∞) = −∞; if r ∈ R, then r+(+∞) = +∞, r+(−∞) = −∞, −∞ < r < +∞. +∞ + (−∞) is undefined. If r > 0, then r · (+∞) = +∞, r · (−∞) = −∞. If r < 0, then r · (+∞) = −∞, r · (−∞) = +∞. And 0 · ∞ = 0.

λ will denote the Lebesgue-measure and also the outer measure as well.
We call f : K → R a simple function, if Ranf is finite.
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.