Author:
(1) CALLA TSCHANZ.
Table of Links
- Abstract and Intro
- Background on tropical perspective
- The expanded construction
- GIT stability
- Stack perspective
- The canonical moduli stack
- References
4. GIT stability
In this section, we set up some results analogous to those of [GHH19] to describe various GIT stability conditions on the scheme X[n] with respect to the possible choices of G-linearised line bundles described in the previous section. In particular, we show that these stability conditions do not depend on the scheme structure of the length m zero-dimensional subschemes, but instead can be reduced to combinatorial criteria on configurations of n points.
4.1 Hilbert-Mumford criterion
In this section, we shall recall the definition of Hilbert-Mumford invariants and give a numerical criterion for stability and semi-stability in terms of these invariants.
Let H be a reductive group acting on a scheme S, which is proper over an algebraically closed field k. Let L be a H-linearised ample line bundle. Then a 1-parameter subgroup of H (denoted 1-PS for convenience) is defined to be a homomorphism

4.2 Action of 1-parameter subgroup


4.3 Bounded and combinatorial weights
In this section, we explain the relation between what [GHH19] call the bounded and combinatorial weights of the Hilbert-Mumford invariants.
Keeping the notation as consistent as possible with [GHH19], let
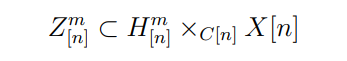
be the universal family, with first and second projections p and q. The line bundle
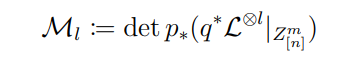
is relatively ample when l ≫ 0 and is G-linearised, exactly as in Section 2.2.1 of [GHH19].
Relationship between bounded and combinatorial weights. The following lemmas describe how the Hilbert-Mumford invariant can be decomposed into a sum of invariants.

Note that, whereas the combinatorial weight depends on the choice of linearised line bundle, the bounded weight does not. Similarly to [GHH19], we can show that the bounded weight, as its name suggests, can be given an upper bound.

The following result is based on Lemma 2.3 of [GHH19], with some slight modifications to suit our setting.

Let us discuss now how the bounded weight affects the overall stability condition. The following lemma is immediate from [GHH19], but we recall their proof here for convenience.

Proof. As we have shown that the bounded weight can be expressed as
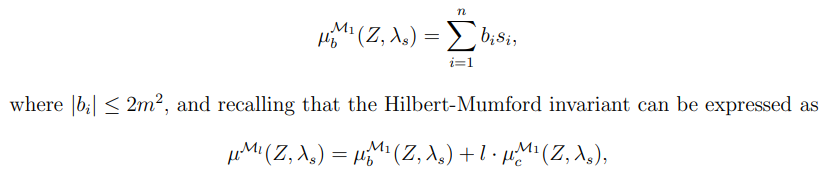
it is just a matter of choosing a big enough value of l to make the combinatorial weight overpower the bounded weight. This allows us effectively to treat the bounded weight as negligible and ignore it in our computations.


Remark 4.3.5. Note, here, that such a Z will not necessarily be smoothly supported, nor will every point of the support of Z necessarily be contained in a ∆-component.
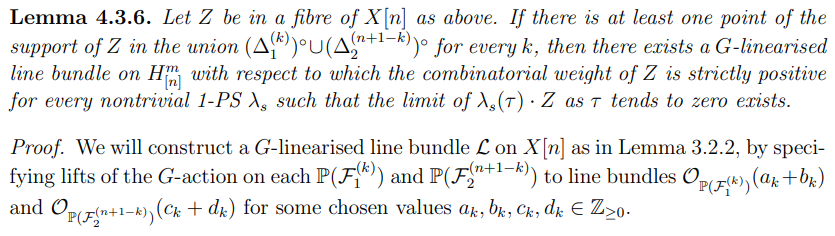

Repeating this process over all k ∈ {1, . . . , n} will give us a description of L and we may form the G-linearised line bundle M from this line bundle in the way described at the start of this section. For more details on why this yields a positive combinatorial weight, see the proof of the following lemma. Note that this is not the only GIT stability condition for which Z is stable.
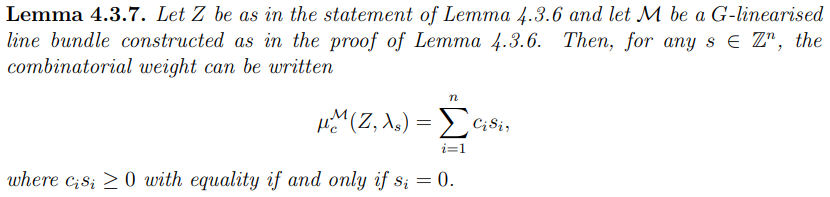
Proof. It is clear that the combinatorial weight may be written as a sum
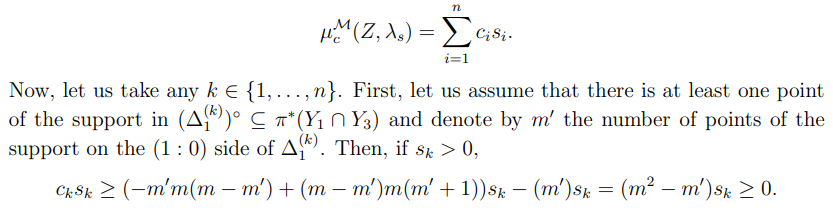

4.4 Semistable locus and GIT quotient
Proof. This follows from Lemmas 4.3.3 and 4.3.7. Indeed, by Lemma 4.3.3, if the combinatorial weight can be written in the form
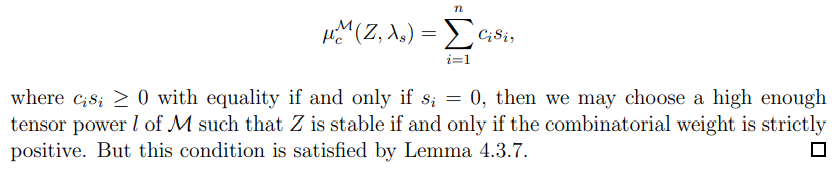

Proof. Let us choose an arbitrary G-linearised line bundle M, not necessarily constructed as above, with respect to which Z has Hilbert-Mumford invariant


Proof. This follows directly from Lemmas 4.4.1 and 4.4.2.
We can now describe the GIT quotients resulting from these constructions. Let
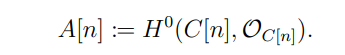
Then we recall from Lemma 3.1.13, the isomorphism
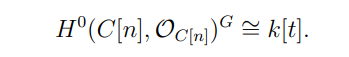
For all choices of linearised line bundle described in the above, the GIT quotient on the base therefore behaves as follows

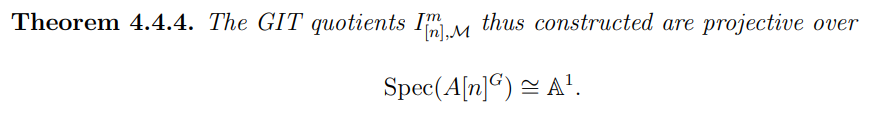
Proof. This result follows directly from the relative Hilbert-Mumford criterion of [GHH15].
This paper is available on arxiv under CC 4.0 license.

